La Relación entre la Regla de los Tercios y la Proporción Áurea.

La Proporción Áurea Explicada con Imágenes

Bien, pues apliquemos todo esto al mundo visual. Creemos un rectángulo cuyos lados midan dos de los números de la serie de Fibonacci:

Y ahora vamos a dividirlo siguiendo la serie numérica:

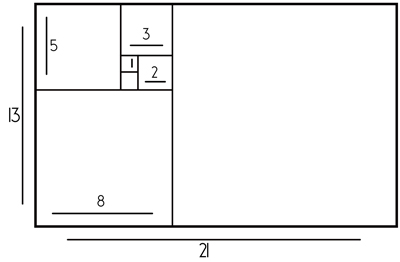
Si dibujamos una línea que una todos estos pequeños recuadros, quedaría algo parecido a esto:

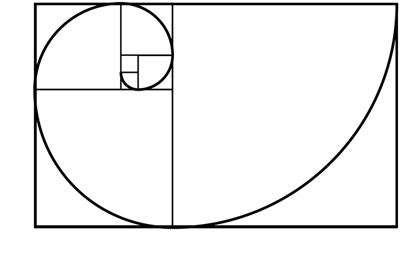
La espiral resultante (conocida como Espiral de Oro o Espiral Aurea) está permanentemente presente en la naturaleza: en las semillas de un girasol, en las conchas marinas... Componer una imagen siguiendo esta espiral nos resulta agradable visualmente porque las proporciones que se obtienen nos parecen naturales.

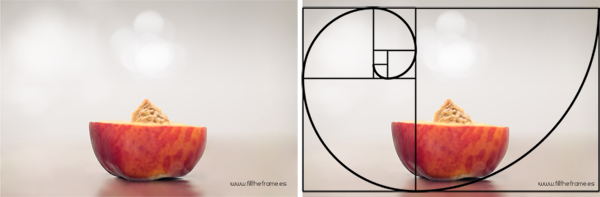
Es importante tener en cuenta que las fotografías no acostumbran a tener unas proporciones áureas (y si se trata de cámaras de medio formato, cuyos sensores suelen ser cuadrados, todavía menos) así que la espiral de Fibonacci debe ser sólo una guía que te ayude a componer y nunca una regla intocable que te cierre puertas creativas. También es cierto que muchas veces, componemos según la espiral de oro sin ser conscientes de ello, simplemente porque la composición que hemos creado nos ha parecido atractiva visualmente. La imagen anterior es un ejemplo de ello, pues la imagen se tomó y luego, para la redacción de este artículo, se le añadió la espiral, momento en el que mi di cuenta de que había seguido la proporción áurea en su composición, sin ni siquiera percatarme de ello.

Siguiendo la proporción áurea puedes tener una idea de dónde situar el horizonte o los puntos más importantes de tu fotografía. Lo importante es ser consciente de que no es una ley que se deba cumplir a rajatabla y de que en absoluto asegura la calidad de la imagen final. A veces puede salir una fotografía más atractiva visualmente rompiendo esta regla que siguiéndola, todo es cuestión de probar. Un claro ejemplo de ello son las imágenes simétricas.

Ya habrás imaginado que todo esto te lo estoy contando con un fin y que, seguramente, ese fin sea llegar al origen de la Regla de los Tercios. Bien, pues ha llegado ese momento. Seguimos con el cuadro que hemos utilizado anteriormente. Lo que hacemos ahora es colocar cuatro espirales en el mismo rectángulo. Colocándoles de manera que se inicie una espiral en cada una de las cuatro esquinas del recuadro:

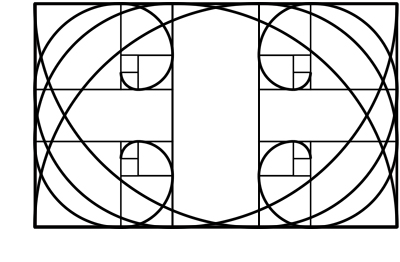
Qué, ¿te suena lo que ves? Vamos a marcar en rojo el centro de las espirales:

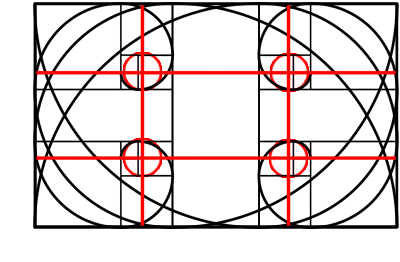
Señoras y señores, ¡aquí tenemos nuestra querida Regla de los Tercios! Así que ha quedado demostrado que las matemáticas nos ayudan a componer fotográficamente. Con este dibujo, además, se ven de manera muy gráfica y evidente, las zonas con más interés visual: las esquinas. Como se puede apreciar en el esquema, el centro de la imagen es la zona "menos interesante" de un encuadre (hablamos en general; como ya hemos descrito anteriormente, existen fotografías que rompen por completo esta concepción y, aún así, son muy atractivas visualmente.)

Como has visto, la regla de los tercios es una versión de la proporción áurea; en general, resulta más sencillo componer una fotografía con la regla de los tercios en mente (o superpuesta en la pantalla de la cámara a modo de guía) que con la Espiral de Oro.